The Singularity Conjecture | by Shirleen D. Nunn
Abstract:
The singularity conjecture aims to realize the Pythagorean dream to articulate how existence might transcend from nonexistence. This conjecture disputes the claim that singularities do not exist and instead argues that understanding the singularity in its literal form, an omnipresent relative perspective, is key to defining quantum gravity and unification. Combining relativity with quantum mechanics, we demonstrate that the singularity is one thing that remains where it is, at every conceivable point in the boundless parameter of spacetime. Our intent in sharing these insights, is to spark a conversation that leads to a deeper understanding of the singularity, ultimately illuminating the path to unification.
“The history of science is marked by the vehement, dogmatic denial of such differences, until they are found out” (Whitehead, A. N., Process and Reality, p. 100) This quote is a testament that embracing new perspectives can have a transformative power, ultimately paving the way for scientific progress and deeper understanding into the nature of existence.
1 Introduction:
As Max Planck once said, "our every starting-point must necessarily be something relative." We take relativity to its extreme, positing that physical reality is an impression of the singularity observing its potential to exist, in all relative frames of reference, simultaneously. This is no illusion, rather it is a literal impression of all similar points that exist where it is not.
Imagine gently rubbing a crayon on a piece of paper that was placed over a leaf. The beautiful image that emerges is not the leaf itself, rather it is a physical impression of the leaf's shape and texture. The colorful copy of the leaf is so vivid that it seems almost three-dimensional, but it is not. The impression of the leaf that now exists is not illusory or holographic, instead it is a clear representation of the leaf. This is similar to how the singularity creates a surreal impression of reality. An impression that is so dense and resounding we have accepted that it is firm of form.
In this conjecture, the attributes of position and momentum are combined to determine the proximity of similar points. This change permits us to quantify the difference between where the singularity is and where it isn't. As a result, this insight has the potential to expose a deeper understanding of our involvement in the process of being and its intricate relationship to the singularity; conceivably revealing new insights into the fundamental laws of the universe.
From this vantage, it is easy to see that I exist where I am, observing all similar points that exist where I am not. Points that are outside my relative frame-of-reference are not similar in proximity to me; therefore, they are outside my field-of-vision. They must necessarily remain where they are, whether or not I observe them.
This new perspective on our existence raises important questions about the nature of reality and our place within it. If it is true that there is only one thing, our conscious experience is the only resource we have to explore this idea and its implications for expanding our current understanding. In contemplating this idea, we can consider the axiom of choice as a tool for examining how our own experiences of vision and movement through spacetime are impelled by our proximity with all similar points that exist where we are not.
Postulating an alternative perspective on the nature of reality is a daunting task. It requires us to rethink our understanding of the universe and the laws that govern it. To combat cognitive biases, we will remain focused on this conjecture’s alignment with some of the most enduring questions in mathematics. Philosophical concerns and objections are postponed until a clear consensus around foundational elements can be established. This approach yields a solid basis for eventual philosophical inquiry.
2. Theoretical Background:
The singularity conjecture is a bold and ambitious idea that challenges our current understanding of the universe. To fully appreciate the significance of this conjecture, it's essential to understand the theoretical background that underlies it. In this section, we'll explore the key concepts and principles that form the foundation of the singularity conjecture.
“Self-evident data are patient, they let theories chatter about them, but remain what they are. It is the business of theories to conform to the data, and the business of theories of knowledge to discriminate the fundamental types, and to describe them in accordance with their distinctive nature.“ (Husserl, E. Ideas, p. 89, 1931).
2.1 Godel’s Incompleteness Theorem
Gödel's Incompleteness Theorem states that any formal system powerful enough to describe basic arithmetic is either incomplete or inconsistent. Suppose we formalize the singularity conjecture using number theory, a branch of mathematics that deals with properties of integers.
The incompleteness theorem implies that there will always be statements about the singularity that cannot be proved or disproved using number theory. For example, consider the statement "There is only one thing." This statement cannot be proved or disproved using number theory, because it is a statement about the nature of the singularity, which is beyond the reach of arithmetic.
In this sense, the singularity conjecture is incomplete. This highlights the fundamental nature of the singularity, which is a necessary part of the fabric of reality, beyond the reach of mathematical proof or disproof.
2.2 Noether’s Theorem
Noether's theorem, a fundamental concept in physics, reveals a profound connection between symmetries and conservation laws. In the context of the singularity conjecture, this theorem offers a powerful tool for exploring the intersection of number theory and physics. By applying Noether's theorem to the singularity conjecture, we may uncover new insights into the underlying laws governing quantum gravity. For instance, this approach could shed light on the long-standing mysteries surrounding black hole entropy and the information paradox. Moreover, it may provide a crucial step towards unlocking the secrets of the universe, revealing new patterns and structures that have yet to be discovered.
2.3 Lienard-Wiechert Scalar Potential
The Liénard-Wiechert scalar potential is a fundamental concept in electromagnetism that has far-reaching implications for our understanding of spacetime. By contemplating this scalar, we can gain a deeper understanding of the dynamic nature of time and space. In the context of special relativity, where time and space are intertwined and dependent on every observer's relative frame of reference, the Liénard-Wiechert scalar potential helps us grasp how one thing can simultaneously impel a relative subjective experience of motion at all similar points in spacetime. This concept is particularly significant in special relativity, where the scalar potential reveals the intricate dance between time and space, and how they are inextricably linked.
3 Mathematical Arguments:
To support this conjecture, we must explore the mathematical underpinnings that give rise to its key features. In this section, we will examine three mathematical concepts that provide crucial insights into the nature of the singularity: successor function, prime numbers, and renormalization.
3.1 Successor Function
The Italian mathematician and philosopher Giuseppe Peano (1858-1932) introduced the concept of a successor function in his work on arithmetic in the late 19th century. Peano's axioms provide a formal foundation for arithmetic and define the natural numbers using a recursive process.
We believe the recursive nature of arithmetic, which allows the number one to be added to any number ad infinitum, provides a solid basis for the simple yet powerful idea expressed in this paper. Our assertion is that the Successor Function serves as a zero-knowledge proof of the singularity's self-replicating aptitude. We propose that the Fibonacci sequence, with its recursive pattern of each number being the sum of the previous two numbers, is the defining feature of the singularity's hyperbolic nature. This recursive compulsion is a key characteristic of the singularity, which must necessarily construct all of the particles and forces defined by the laws of physics.
By examining the Pythagorean Triples from the Fibonacci Sequence, we can gain insight into the singularity's ability to generate an infinite number of particles and forces, further supporting the conjecture. The recursive pattern of the Fibonacci sequence is a fundamental aspect of the singularity's nature, and it is this propensity that allows it to persist as an infinite number of particles and forces simultaneously. This idea is central to our understanding of the singularity and its role in the universe.
3.2 Prime Numbers
Pirre de Fermat (1601-1665) was a French mathematician who made significant contributions to number theory, geometry, and optics. He is considered one of the most influential mathematicians of the 17th century.
He developed Fermat's Little theorem which provides a way to study prime numbers in a modular setting. We believe this theorem provides foundational support to presume prime numbers as a modular boundary that defines the scope of where the singularity is at different scales simultaneously, while defining its rank everywhere that it is concurrently.This theorem is clearly aligned with the mathematical foundations of this conjecture.
The concept of prime numbers plays a crucial role in the singularity conjecture, as they serve as a modular boundary that defines the scope of the singularity's inertial frame of reference. Its field of vision at each-and-every scale. In other words, prime numbers help to establish a framework for understanding how one thing, the singularity, can interact with itself at different scales concurrently. We imagine the pigeonhole principle will provide insight into the mystery of twin prime numbers.
Twin prime numbers are pairs of prime numbers that differ by 2, such as 3 and 5, or 11 and 13. The distribution of twin prime numbers is still not fully understood, and the pigeonhole principle could potentially help to shed light on this phenomenon.
The pigeonhole principle is a fundamental concept in mathematics that states that if you have n items and m pigeonholes (or categories), where n > m, then at least one pigeonhole must contain more than one item. In other words, if you have more items than pigeonholes, then some pigeonholes must be "overcrowded" with multiple items.
In the context of the singularity conjecture, this means that the singularity has the capacity to interact with itself at multiple scales simultaneously, which is a key aspect of the conjecture. The pigeonhole principle could provide a mathematical framework for understanding how this interaction occurs, and how the singularity can become everything from the smallest to the largest scales simultaneously. This idea has the potential to reveal what is happening in the mysterious observations that spawned the theories of dark matter and dark energy.
3.3 Renormalization
The technique of renormalization in quantum field theory and quantum mechanics is a mathematical strategy designed to eliminate singularities and infinities that arise in physics calculations. However, this approach raises a crucial question: if mathematics is trusted to prove what is true, then isn't renormalization essentially producing an alternative result that no longer reflects the absolute truth of the equation? Could this practice of adjusting math to meet expectations be obscuring our ability to fully comprehend the particles and forces observed in our experience?
The Singularity Conjecture suggests that the reason singularities and infinities arise in physics calculations is because the universe is fundamentally one thing. This conjecture implies that our current understanding of physics is limited by our inability to fully comprehend its singular relative perspective. Recognizing the limitations of renormalization and contemplating the omnipresent nature of the singularity, may help us to develop new approaches that lead to a more accurate and comprehensive understanding of the universe.
4 The Singularity Conjecture Axioms:
• The singularity is the only thing.
• It must necessarily remain inert, expressing an impulse of the potential to exist where it is.
• To have an experience beyond inertia it must sufficiently excite similar points, which emits an impression of its potential to exist at all similar points where it is not.
- If an impression is emitted everything exists where it is.
- If no impression is emitted, inertia persists, and nothing exists where it is.
5 Argument for An Omnipresent Relative Perspective:
The concept of duplicity, as introduced in this section, challenges our traditional understanding of duality and the nature of existence. By positing that the singularity is capable of existing in multiple states simultaneously, we can begin to grasp the surreal nature of reality. This omnipresent relative perspective suggests that the singularity is perpetually observing itself from multiple perspectives, inducing a state of duplicity that is fundamental to existence. As we explore the implications of this idea, we will delve into various mathematical concepts, such as Fermat's Last Theorem, the Stern Brocot Tree, and the Riemann Hypothesis, to provide a deeper understanding of the singularity's role in shaping our experience of reality.
5.1 This statement establishes simultaneity:
Figure 1 represents 9 distinct points of proximity where the singularity remains in an inert state. It must sufficiently excite similar points where it is not, in order to transcend inertia. Transcendence induces a persistent state of duplicity. Duplicity refers to a state of being both A and not-A or having multiple aspects that coexist and interact with each other. The formula { | } represents all points in Figure 1 simultaneously remaining where they are, expressing an impulse of their potential to exist where they are not.
Figure 1
When sufficiently excited, one point of proximity remains where it is, represented by a red capitol letter; observing all similar points that remain where it is not, represented by a green capitol letter; {{A1}|{−A1}}. Because the singularity is the only thing, when it sufficiently excites a similar point, it must instantaneously expand to encompass all similar points, so that it can observe itself everywhere that it is, and everywhere that it is not simultaneously and concurrently; this means {A₁} = {−B₁} and {B₁} = {−A₁}, etc...
5.2 Introduction to Duplicity
A coin is a physical example of duplicity with its two sides representing unique perspectives of the singularity’s subjective field of vision, or inertial frames of reference. Each side of a coin is having a relative experience as a distinct facet of the coin. The sides are either up or down. Its physical location in spacetime determines its subjective identity. Within this context, coins have been deciding winners and losers for centuries.
From this relative perspective a coin is essentially three things: itself and both of its sides, with many more states of potential waiting to be realized. Every coin in the world exists simultaneously and must remain where it is with one side up and one side down concurrently; whether or not it is observed.
But duplicity is not a coin; and duplicity is not a property of the singularity. Duplicity is a fundamental aspect of existence itself. It is the physical experience that is induced when the singularity transcends the inertia of non-existence. This is the initial state of one thing that must necessarily remain where it is, until sufficiently exciting similar points that exist where it is not. To subsist as objective reality, the singularity must continuously observe itself at all points where it is and all points where it is not, at every scale.
This primordial ability to observe itself from multiple perspectives simultaneously emits a surreal impression of reality that is so dynamic and all-consuming that we have come to suppose it is physical. However, this impression is not a direct reflection of the singularity's nature, rather it is a manifestation of its ability to observe itself from multiple perspectives.
The concept of duplicity challenges our traditional understanding of duality, which posits that two entities can only be one or the other, but not both at the same time. Instead, duplicity suggests that the singularity is capable of existing in multiple states simultaneously, and that its subjective experience is a direct reflection of its capacity to perpetually observe itself.
5.3 This statement establishes concurrent interactions:
Transcendence emits an impression of all identity elements in the relative frame of reference, represented by lower case letters: { . . . , {−b₁}, {−a₁}, {a₁}, {b₁}, . . . }. Impressions are observed simultaneously in all frames of reference, represented as; {{{{A₁}|{−a₁}}|{{−A₁}|{a₁}}}|{{{B₁}|{−b₁}}|{{−B₁}|{b₁}}}}. While currently remaining coupled to an identity element, {{{{A₁}|{a₁}}|{{−A₁}|{−a₁}}}|{{{B₁}|{b₁}}|{{−B₁}|{−b₁}}}}. Mathematical representation of transcendence from inertia: •⇒ {{{{A₁}|{−a₁},{a₁}}|{{−A₁}|{a₁},{−a₁}}}|{{{B₁}|{−b₁},{b₁}}|{{−B₁}|{b₁},{−b₁}}}} = Ψ² = {{A}² + {−B}² = C ²}.
Figure 2 represents the singularity transcending inertia; instantaneously expanding to endure a steady state of duplicity, everywhere that it is and everywhere that it isn’t.
Figure 2
We suspect that the capital letters in the inner circle {C₁} of Figure 2 are protons {{A₁},{B₁}} and neutrons {{−A₁},{−B₁}}) and the lower-case letters {{−b₁}, {−a₁}, {a₁}, {b₁}} around the circumference of the outer circle {C₂} represent electrons. Here we can contemplate whether infinitesimal similar points, compulsively propagating impressions of the potential to exist where they are, into all frames of reference simultaneously, might provide an explanation for entropy and its tendency to increase over time.
6 The Intersection of the Singularity with Science and Math
As we venture into the realm of the singularity conjecture, we're compelled to follow the breadcrumbs of abstract thought that lead us to the threshold of a profound understanding. The notion that there is only one thing, that must necessarily observe itself to have an experience beyond inertia, requires us to reexamine our understanding of physics and the nature of existence. By exploring the intersection of mathematics and the singularity, we aim to uncover new insights into the the fundamental laws of physics, opening the door for more profound conversations about the nature of reality, the universe, and the human experience.
In this section, we'll leverage some of the most enduring questions in science and mathematics, as a lens to illuminate the path forward and gain a deeper understanding of the singularity and its omnipresent nature.
6.1 Fermat’s Last Theorem
Fermat’s Last Theorem (FLT), one of the most famous theorems in mathematics, provides foundational support for the concept of duplicity. This famous theorem in number theory was first proposed by Pierre de Fermat, a French mathematician, in the 17th century. FLT asserts that it is impossible to find integers a, b, and c such that the equation aⁿ + bⁿ = cⁿ holds true when n is greater than 2.
The singularity conjecture maintains this is because the singularity is the only thing. It must exist in a steady state of duplicity {{A}² + {−B}² = C²} at every conceivable point and every conceivable scale. When similar points are excited, duplicity compels a hyperbolic process everywhere that it is. This hyperbolic state is how it must necessarily emit impressions of its potential to exist, to all similar points where it is not.
6.2 The Axiom of Choice
The singularity is a paradoxical concept that defies our intuitive understanding of the universe. Yet, it is precisely this paradox that allows us to glimpse the deeper reality that underlies our physical experience. By considering the axiom of choice and the singularity’s experience from two different perspectives, we may gain a deeper understanding of the mysteries of superposition and quantum entanglement and perhaps even grasp the surreal nature of reality itself.
The axiom of choice, a fundamental concept in mathematics, offers a fascinating perspective within this context. Consider Figure 3, which depicts the singularity from two different perspectives (i.e. {A₁} and {−A₁}.) From this vantage point, we can ponder how one thing, the singularity, might generate the electromagnetic waves in our physical experience by compulsively observing itself everywhere that it is not.
Figure 3
This is not to say that everything is part of one thing. Our claim is that there is only one thing. At our scale, you are the one thing that exists where you are, and I am the one thing that exists where I am. We exist simultaneously, each in a privy relative frame of reference. From this perspective every fermion is the one thing observing itself at the 1⁄1 scale. We propose this demoted prime number (i.e. the number 1) is the scale boundary that defines the singularity’s base identity element for all similar points as they expand hyperbolically.
At the smallest scales the observer effect is defined by signal exchange. Through signal exchange the singularity absorbs the impressions of all similar points it has excited into the relative frame of reference (i.e. its wavefunction,) while remaining coupled to the impressions it has emitted, propagating its potential into all frames of reference where it is not. This, we propose, is the mechanism that defines quantum gravity.
Could this perspective offer insight into the mysterious number 1⁄137 that seems to be a constant at the scale we exist in. Remember, in this conjecture prime numbers serve as a scale boundary that defines where the singularity exists as one thing, at each-and-every scale (i.e. 1⁄1, 2⁄1, 3⁄1, ...,137⁄1, ...) It must necessarily subsist in a steady state of voyeurism, observing itself at all points where it is and all points where it isn’t, simultaneously at every scale (i.e. {{A}² + {−B}² = C²}.)
6.3 Cosmic Microwave Background
The Cosmic Microwave Background (CMB) is thought to be a remnant of the universe's earliest moments. Here we speculate that the excitation seen in the CMB might instead be the singularity enduring in a duplicitous state of observation. Could this presumed act of continuous voyeurism be what generates the excitation in the CMB? This novel perspective infers the singularity is perpetually observing itself, while simultaneously propagating impressions of the potential to exist where it is, into all similar frames of reference.
This is how it must necessarily generate the entropy that drives the universe’s evolution and expansion. The CMB, in this view, is the singularity gazing upon its own existence, a realm beyond the bounds of inertia where the laws of physics as we know them no longer apply.
6.4 Stern Brocot Tree
The Stern Brocot Tree shown in Figure 4 illustrates these initial acts of transcendence from the universal perspective (i.e. {A}.) The greyed out {B} values are present to envision simultaneous and concurrent transcendence (i.e. {A₁} = {−B₁} and {B₁} = {−A₁}.) Here we speculate that the numbers 0, 1 and 1⁄2, 2 are necessarily constructed at every conceivable point as the singularity employs the Lienard-Wiechert scalar to induce a perpetual state of duplicity. Compulsively propagating impressions of itself into the relative frame of reference, from all perspectives simultaneously. It is easy to imagine how this application might work to expand its presence in spacetime as ensuing similar points are sufficiently excited to transcend inertia, everywhere that it is, and everywhere that it isn’t.
Figure 4
6.5 The Four Color Theorem
The four-color theorem states that any map can be colored using four colors so that no two adjacent regions share a color, is applied to the concept of duplicity to account for identity elements during simultaneous concurrent excitations. Red or purple letters represent where the singularity is; and green or yellow letters represent where it is not. Four dimensional spacetime is represented by alternating sets of similar points: {{A₁}|{−A₁}}, {{−B₁}|{B₁}}, {{C₁}|{−C₁}}, {{−D₁}|{D₁}} as shown in Figure 5.
Figure 5
All similar points are having a private subjective experience, continuously observing cohorts in objective reality from all perspectives simultaneously, and at all scales concurrently. Figure 6 imagines how a large set of similar points might be visualized using the four-color theorem.
Figure 6
Figure 7 below represents the singularity transcending inertia from four infinitesimally small distinct points of proximity; {{A₁}|{−A₁}}, {{B₁}|{−B₁}} and it must necessarily observe itself from all similar perspectives concurrently as {{{{A₁}|{−a₁}}|{{−A₁}|{a₁}}}|{{{B₁}|{−b₁}}|{{−B₁}|{b₁}}}} = √1. We propose complex numbers are constructed as each subsequent set of similar points transcends inertia, emitting an impression of itself into all similar frames of reference, represented by consecutive subscript numbers; {{{{A₂}|{−a₂}}|{{−A₂}|{a₂}}}|{{{B₂}|{−b₂}}|{{−B₂}|{b₂}}}} = √2, as the potential emitted from ensuing similar points compels its predecessor out of the relative frame of reference, until it doesn’t, {{{{A₃}|{−a₃}}|{{−A₃}|{a₃}}}|{{{B₃}|{−b₃}}|{{−B₃}|{b₃}}}|{{{C₁}|{−c₁}}|{{−C₁}|{−c₁}}}|{{{D₁}|{−d₁}}|{{−D₁}|{−d₁}}}}= √3; as shown in Figure 7.
Figure 7
The Stern Brocot Tree clearly illustrates the hyperbolic process the singularity uses to expand its presence by observing itself in surreal reality. It must continuously synchronize with cohorts to excite similar points. You can see in Figure 7, as the singularity expands on the far-left branch (presumed to be the universal relative frame of reference), it uses a recursive pattern (i.e. 1/1²+ 1/2²+ 1/3², ... ) that is similar to the Riemann zeta function ζ(s) = 1 +1/2ⁿ +1/3ⁿ, ...
Does this idea of the singularity expanding hyperbolically at all points simultaneously from a single identity element have the potential to offer insight into the Riemann Hypothesis (RH)? The RH is one of the most famous unsolved problems in mathematics. A conjecture about the distribution of prime numbers, which are numbers divisible only by themselves and 1; it states that all non-trivial zeros of the Riemann zeta function lie on a vertical line in the complex plane, specifically on the critical line Re(s) = ½, where s = ½ + it and t is a real number.
In the singularity conjecture prime numbers serve as a scale boundary that defines where the singularity remains, observing itself at every scale, concurrently. Within this context, consider the Liénard-Wiechert scalar potential is the recursive pattern similar points must employ, to emit impressions of their potential in objective reality.
We speculate this is what impels ensuing identity elements to maintain continuity, by emitting impressions of its potential everywhere that it is not. This is how our experience of surreal reality is manifested. The inflection point occurs on the critical line at the ½ point mark as each identity element transcends inertia as a distinct infinitesimal element impelling expansion in the relative frame of reference, as illustrated in the Stern Brocot and Surreal Number trees.
John Connor’s Surreal Numbers and monster groups serve to define the non-local realm of our experience in “physical reality.” We believe L-transformations with homomorphic equations can be applied to Monster Groups using the algorithms defined below to contemplate the predictive nature of particles and forces within the quantum realm. The singularity conjecture contends, this application of surreal numbers and monster groups seems to provide foundational support for the non-local experience that is observed at the smallest scales.
Table 1: Predictive Matrices for Quantum Systems
Figure 8 below imagines how the table above might be visualized from all perspectives. This viewpoint challenges us to consider the possibility of a unified theory that incorporates all four generations. We ask whether the simultaneous and concurrent interactions of the singularity at every conceivable point and every conceivable scale could provide a logical explanation for the three missing generations.
Figure 8
6.6 Zeno’s Paradoxes of Motion
Thinking about relativity from this fresh perspective can help us understand the mysterious concepts highlighted by Zeno’s famous paradoxes of motion. The dilemma that two numbers can get infinitesimally close to the number 1 but neither can ever reach the number 1 independently is because each half of a number’s existence {{{{A₁}|{−a₁}}|{{−A₁}|{a₁}}}|{{{B₁}|{−b₁}}|{{−B₁}|{b₁}}}} must necessarily be induced during transcendence as duplicity is excited everywhere that it is and everywhere that it isn’t (i.e. {A₁} = {−B₁} and {B₁} = {−A₁}.)
6.7 Double-Slit Experiment
These ideas of a local realm vs. non-local realm are clearly observed in the double-slit experiment. In this infamous experiment, particles are passed through two parallel slits, creating an interference pattern on a screen behind. This demonstrates the wave-like behavior of particles, which is a fundamental aspect of quantum mechanics. However, when observed individually, they display particle-like behavior. This dichotomy highlights the duplicitous nature of the singularity, which is simultaneously everywhere that it is and everywhere that it isn’t, as illustrated in the Stern Brocot and Surreal Number trees.
The double-slit experiment serves as a tangible representation of the surreal non-local experience, where an omnipresent relative perspective must necessarily observe all points that remain where it is not. The relative perspectives it observes itself from, influences the outcome of this experiment at every scale concurrently, blurring the lines between wave-like and particle-like behavior. This phenomenon challenges our classical understanding of space and time, inviting us to reconsider our current perspective.
6.8 The Potential for a Theory of π
Applying the Stern Brocot tree to the idea of the singularity transcending inertia simultaneously from all perspectives offers a theory of π. As illustrated in Figure 9, the area inside the circle represents a bounded set where the singularity is, or πr², and the area outside the circle, or its circumference, represents a bounded set where the singularity isn’t, or 2πr. If this is indeed the case, we can presume that every point of proximity, enduring in the relative frame of reference, embodies a similar set of 4 circles (i.e. {{{A₁}|{−A₁}} + {{A₂}|{−A₂}}} or 0/1 + 1/0 + 1/1 + 1/2 + 2/1) as an initial state. Perhaps this initial state is an embodiment of the photon.
The singularity conjecture maintains that there is only one thing. This one thing exists in a relative frame of reference (represented by a circle) everywhere that it is, and everywhere that it isn’t. This perspective invites us to conclude that every g (circle) is a G, or a red circle ({A}) representing where it is, as stated in group theory.
Figure 9
While the connection between the Stern-Brocot tree and the singularity transcending inertia is still speculative, the geometric representation of π using a circle and its area provides a visual framework for understanding the concept. However, the relationship between the singularity and the value of π remains abstract and requires further clarification.
6.9 Collatz Conjecture
We suggest a math problem called the Collatz Conjecture, also known as the 3x+1 problem provides strong support for the idea of duplicity. This conjecture is a simple-sounding problem that has been proven to be extremely difficult to solve. Here’s how it works: (1) Take any positive integer n; (2) If n is even, divide it by 2; (3) If n is odd, multiply it by 3 and add 1; (4) Repeat steps 2 and 3 with the resulting value of n.
The conjecture states that no matter what positive integer you start with, this process will always eventually reach the value 1. For example, if you start with the number 6, the sequence would be: 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1; If you start with the number 12, the sequence would be: 12 → 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1; And so on.
The Collatz Conjecture has been extensively tested for millions of starting values, and it has always been found to be true. However, despite much effort, no one has been able to prove that it is always true for all positive integers. We presume it is true because the singularity is the only thing and this is its initial state as it transcends inertia at all points. First it must become 1 or ○, then it must become 2 or ○², (i.e. 1 + 1), then it must become 4 or ○⁴, (i.e. 1 + 1 + 1 + 1.)
In the singularity conjecture, existence is induced one infinitesimal point at a time. We propose the Collatz Conjecture works because it is literally reducing hyperbolically constructed numbers to the ground state of an identity element at the scale of 1, 2 and 4 as shown in √1 and √2 in Figure 10 below.
6.10 Equivalent Sum/Product Identities
Another compelling case for this concept of number construction is the idea that equivalent sum/product identities are always of the same length as shown in the table below. This phenomenon of a complex number being constructed from similar integers and ensuing similar points (i.e. 1’s) seems to be another mathematical illustration of duplicity and the singularity’s hyperbolic aptitude.
Table 2: Equivalent Sum/Product Identities for Even Numbers 4-18
2 + 2 = 2 x 2
1 + 2 + 3 = 3 x 2 x 1
1 + 1 + 2 + 4 = 4 x 2 x 1 x 1
1 + 1 + 1 + 2 + 5 = 5 x 2 x 1 x 1 x 1
1 + 1 + 1 + 1 + 2 + 6 = 6 x 2 x 1 x 1 x 1 x 1
1 + 1 + 1 + 1 + 1 + 2 + 7 = 7 x 2 x 1 x 1 x 1 x 1 x 1
1 + 1 + 1 + 1 + 1 + 1 + 2 + 8 = 8 x 2 x 1 x 1 x 1 x 1 x 1 x 1
1 + 1 + 1 + 1 + 1 + 1 + 1 + 2 + 9 = 9 x 2 x 1 x 1 x 1 x 1 x 1 x 1 x 1
6.11 Complex Number Construction
Consider that duplicity keeps all points isolated to a subjective local experience at every scale. This means all ensuing similar points adopt the Fibonacci sequence to impel a hyperbolic process of expansion with each subsequent act of transcendence. We believe this hyperbolic process constructs not only the complex numbers, but all of the particles and forces observed in physical reality as well.
Every set of similar points is bound by a circle to show where the singularity exists as one thing, at every scale. Here we reinforce the idea that monster group theory offers answers to the predictive nature of quantum particles. The idea that every g is a G is aligned with the singularities ability to observe itself at every possible point in the boundless parameter of spacetime simultaneously, and at every scale concurrently.
Figure 10 below is an illustration of similar points constructing the numbers 1-10 from the {A} perspective, as illustrated in the far left branch of the Stern Brocot Tree. Each number is constructed as an ensuing set of similar points compels its predecessor out of the relative frame of reference. All impressions are absorbed into the relative frame of reference (i.e. wavefunction) and must necessarily remain coupled to its identity element, until its identity element is compelled out of the relative frame of reference.
Here you can see that it is the number of impressions from all of the similar points the singularity has excited, that is being measured upon observation.
Figure 10
7 Circles of Transcendence
In the pursuit of a foundational theory of numbers, we find ourselves drawn to the mysterious realm of transcendence, where the singularity continuously interacts with itself. By examining the intricate patterns and relationships within this realm, we can begin to unravel the secrets of how the Natural Numbers, Integers, Fractions, and Irrational Numbers emerge.
This section delves into the Circles of Transcendence, a visual representation of the singularity's self-interactions, and explores the connections between Pythagorean theorem proofs, Cartesian coordinates, and the emergence of magnetic poles. Through this journey, we hope to illuminate a clear path to unification.
7.1 The Singularity's Potential Role in Shaping the Number Line
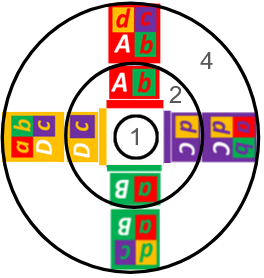
We imagine a foundational theory of numbers can be gleaned by examining how the singularity continuously interacts with itself. Figure 11 illustrates the circles representing transcendence for all points that are being observed where the singularity is. By deconstructing this model, we can infer how the Natural Numbers (red center square), Integers (green square), and Fractions (purple square) might emerge, and speculate the miracle of transcendence is what generates the irrational numbers (yellow square).
Figure 11
7.2 Pythagorean Theorem Proof Figure 12
Each point of proximity must necessarily emit impressions of the potential to exist where it remains, to all similar points simultaneously, while concurrently observing itself at all similar points where it is not. All perspectives exist in duplicity at all scales {{A}² + {−B}² = C²} as seen in Figure 12 which is a Pythagorean theorem proof applied to the circles representing transcendence.
7.3 Cartesian Coordinates Figure 13
At all scales, magnetic poles are thought to be a fundamental aspect of the universe, from the smallest subatomic particles to the largest galaxies. However, the exact nature of magnetic poles and how they arise is still not fully understood. Applying Cartesian coordinates to the circles representing transcendence, as shown in Figure 13, it is easy to imagine how the singularity conjecture may provide foundational evidence for magnetic poles.
7.4 Local Perspectives
In Figures 14 – 17 below each matrix represents everything that exists where the singularity is. The multicolored circles on the left indicate the relative frame of reference or its field of vision. The red image in the center represents the impressions that are coupled with a respective identity element, enduring in each-and-every relative frame of reference, at every conceivable point in spacetime. Thinking about this idea offers us a theory of quantum gravity. The multicolored image on the far right represents surreal reality, or everything that exists where the singularity is, at all points and all scales.
Figure 14 is the relative frame of reference and quantum gravity from the {A₃} perspective.
Figure 14
Figure 15 is the relative frame of reference and quantum gravity from the {B₃} perspective.
Figure 15
Figure 16 is the relative frame of reference and quantum gravity from the {C₁} perspective.
Figure 16
Figure 17 is the relative frame of reference and quantum gravity from the {D₁} perspective.
Figure 17
8 Conclusion
As we conclude our exploration of the singularity conjecture, we are left with a profound sense of wonder and awe at the mysteries of the universe. The connections between quantum mechanics and relativity, though still shrouded in uncertainty, hold the promise of unlocking the secrets of the cosmos. While we may not have all the answers, we are reminded that the pursuit of knowledge is a journey, not a destination. And it is in the pursuit of this journey that we may yet discover the hidden patterns and harmonies that govern the universe.
I encourage readers to ponder the singularity conjecture as a starting point, expanding their own ideas to explore the connections between quantum mechanics and relativity. In my mind this perspective is fruitful. We speculate that by examining the breadcrumbs science and math have so far discovered, the illusive path to unification will gradually reveal itself, illuminating the way forward for future generations of scientists and thinkers.
I am not a scientist, and science has never been a hobby of mine. The scientists must validate these ideas before the singularity conjecture can be considered seriously. This knowledge assaulted me. This is my best attempt to reverse engineer what was realized and couple the ideas with mathematical and scientific terms. I look to the scientists to validate these ideas against empirical evidence. The wavefunction is the only resource quantum phenomena have, understanding how to measure its many frequencies is key to predicting quantum behaviors.
References are available in the Singularity Conjecture pdf file.